This post is a functional Jupyter notebook that enables the user to calibrate an sCMOS camera. It uses pycromanager and micromanager to collect calibration data, and then Python code to analyze that data and video the calibration parameters. In general, it is equivalent to the approach used by Huang et al. below. The cells are filled with data from a calibration of a Hamamatsu BT Fusion sCMOS camera in fast mode.
Cameras
This section describes the math behind a camera in familar terms.
Assume that are incoming photons impinging upon a single detector (i.e., on of the pixels of an sCMOS camera). The rate of those incident photons per measurement is
\[ \lambda = \lambda^\prime + \lambda^{\prime\prime} t,\] where we have denoted a time independent contribution with one prime and a time-dependent contribution with two primes.
For any given time period, the probability distribution function (PDF) of the actual number of photons hitting the detector, \(N\), will be Poisson-distributed with rate \(\lambda\) such that
\[ p(N \mid \lambda) = \text{Poisson}(N\mid\lambda) = \frac{\lambda^N e^{-\lambda}}{N!}.\]
without losing generality, we’ll switch to using electrons instead of photons. A good camera will have a high QE, so most of the incident photon will be converted into photoelectrons, however there are also electrons generated by the camera read process (read noise) and things like (time dependent) dark-currents. So, assuming that \(N\) electrons are generated on the camera pixel in question (regardless of their origin…), a camera will return a number in digital units (DU) corresponding to the number of electrons that were detected. The output signal, \(y\), is generally offset from 0 by some fixed number \(y_0\) to avoid ‘negative’ numbers in unsigned int output of the ADC. This offset addition is a deterministic process, so we can consider the camera to take a number of electrons \(N\) and return a number \(y-y_0\) in DU. That process is stochastic, and generally follows a normal distribution such that
\[ p(y-y_0 \mid N, \theta) = \mathcal{N}(y-y_0 \mid gN, \sigma^2), \]
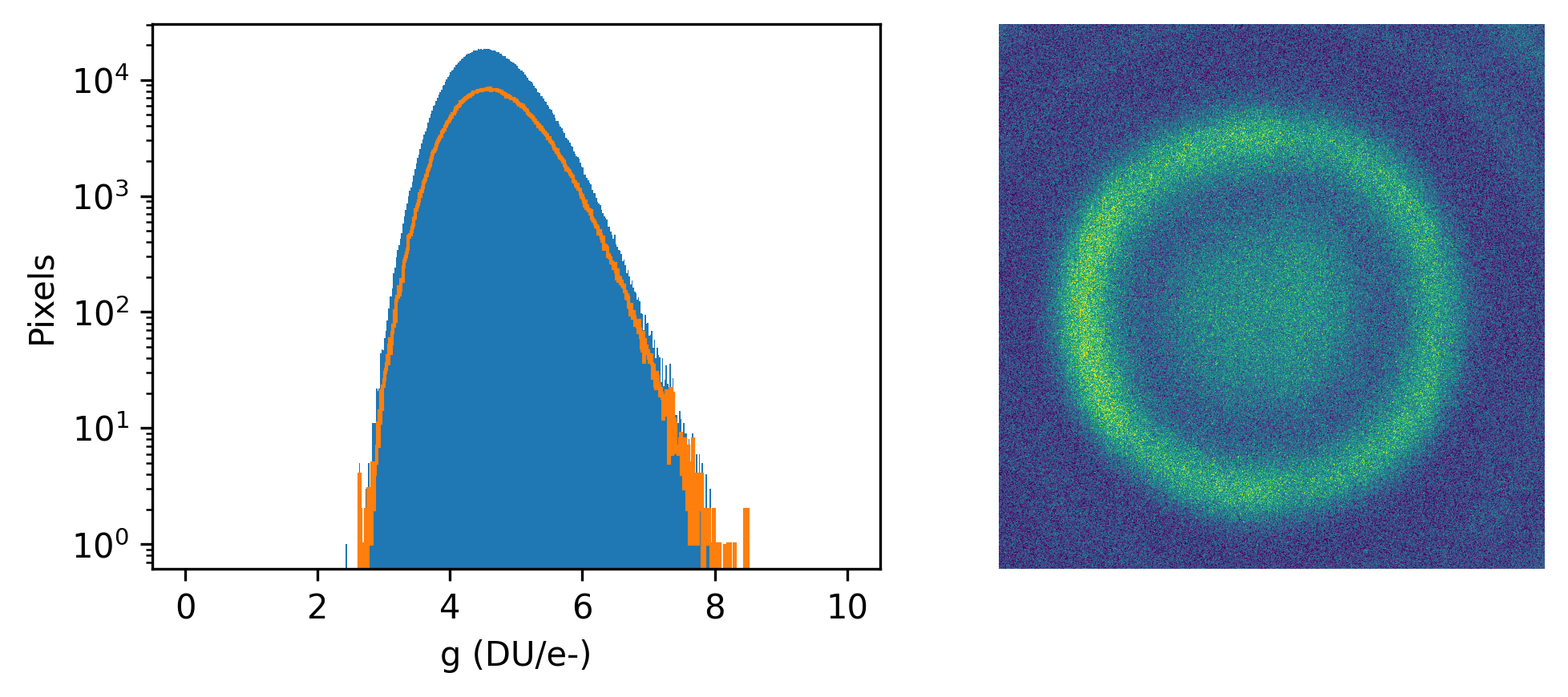
where \(g\) is the gain in \(DU/e^{-}\), \(\sigma^2\) is the read noise, and \(\theta\) is a shorthand for the set of model parameters included in the conditional dependency of a statement (e.g., \(g\), \(\sigma^2\), and \(y_0\) here).
What we’re actually interested in is the PDF of \(y\) as a function of \(\lambda\) regardless of the actual number of \(N\). To get this, we have to perform a marginalization
\[ p(y-y_0 \mid \theta) = \sum_N p(y-y_0\mid N,\theta)\cdot p(N\mid\theta). \]
This marginalization calcuation can be performed analytically in the case that \(N\) is relatively large (ie, greater than ~1000). In that situation the Poisson distribution can be approximated as a normal distribution, such that
\[ \text{Poisson}(N\mid\lambda) \approx \mathcal{N}(N\mid \lambda,\lambda), \] i.e., where the mean and variance of the normal distribution is the rate of the Poisson distribution. This approximation is apparent by moment matching, and more rigorously achieved by comparing the moment generating functions of the Poisson and normal distributions.
In that situation, after integrating over N and a lot of rearranging, we find that
\[ p(y \mid \theta) = \mathcal{N}\left(y \mid g\lambda^{\prime\prime}t + (y_0 + g\lambda^\prime), g^2\lambda^{\prime\prime}t + (\sigma^2 +g^2\lambda^\prime)\right), \]
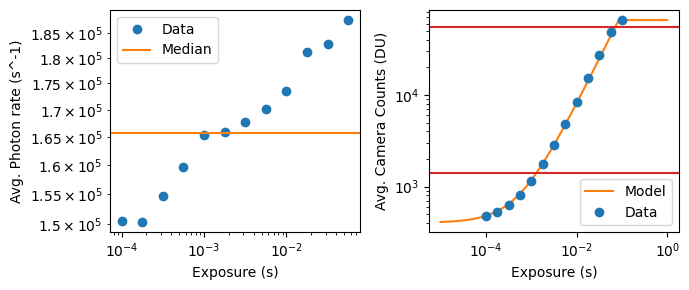
which explicity notes the time dependence of these measurements. It’s important to note that while the mean scales as \(g\) and the variance scales as \(g^2\), both linearly scale with \(\lambda^{\prime\prime}\). In short, both the mean and the variance of the output signal of a camera pixel (under relatively high electron counts) are linear in exposure time.
When comparing to the work of Huang et al. in their SI sections one and two, we note that their sCMOS calibration protocol utilizes the same assumptions. Thus, we have the following equivalencies
| \(g_i\) |
\(g\) |
| \(o_i\) |
\((y_0 + g\lambda^\prime)\) |
| \(var_i\) |
\((\sigma^2 +g^2\lambda^\prime)\) |
| \(v^k_i - var_i\) |
\(g^2 \lambda^{\prime\prime}t\) |
| \(\bar{D^k_i}-o_i\) |
\(g\lambda^{\prime\prime}t\) |
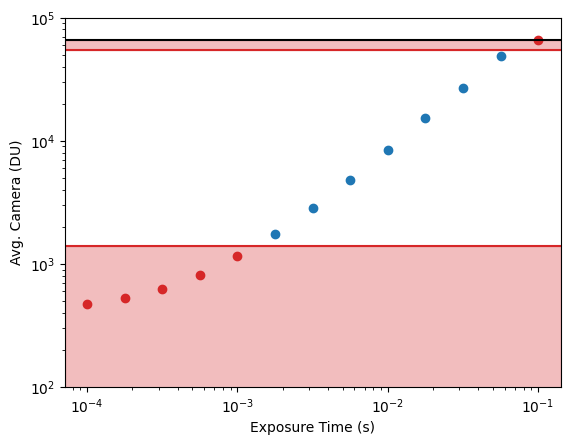
Thus these calibrations are completely equivalent, although our parameterizations are little more transparent. However, instead of using their exact protocol, we provide a more convenient calculation to get \(g\). Note that if \(t = 0\) and/or \(\lambda^{\prime\prime}=0\) (i.e., a dark movie), then we expect
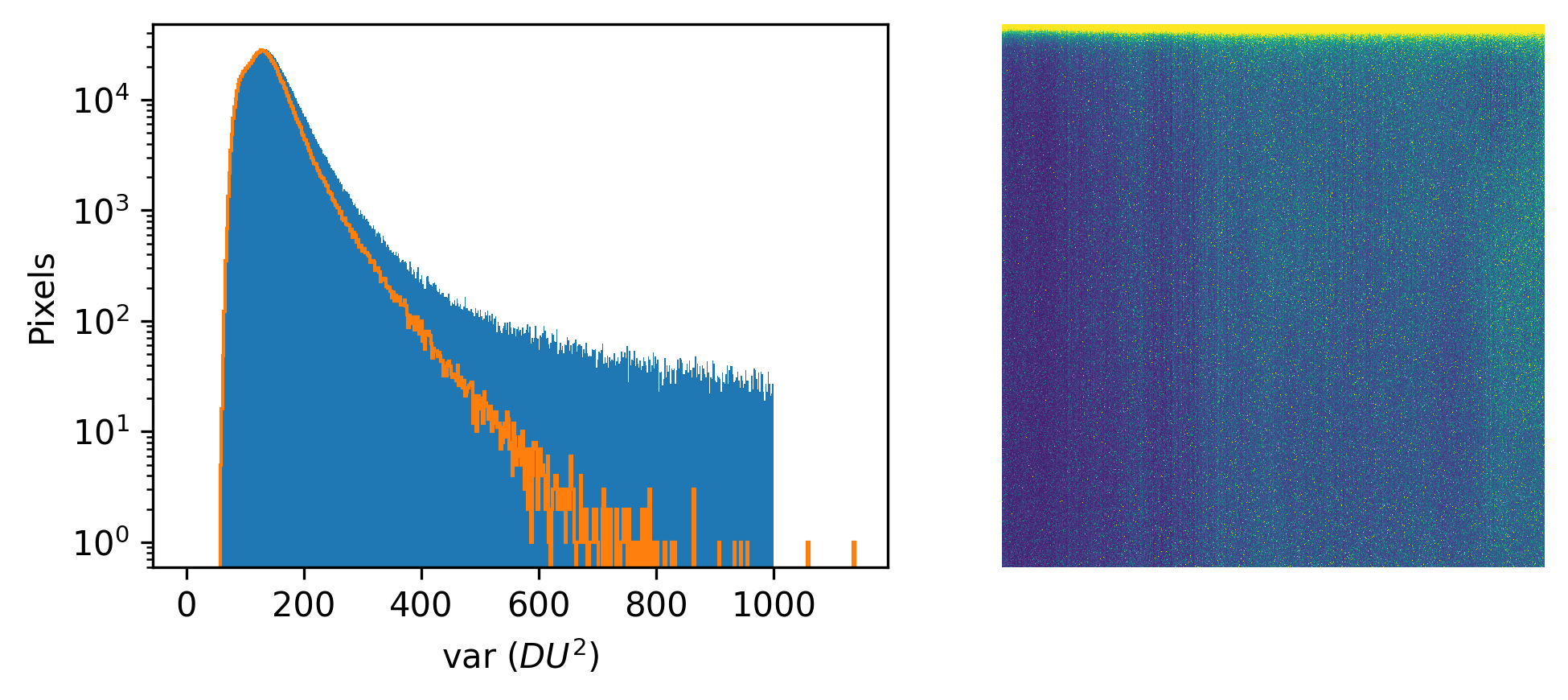
\[ p(y_{i,\text{dark}} \mid \theta) = \mathcal{N}(y_{i,\text{dark}} \mid o_i, var_i), \] so we can obtain measurements of \(y_{i,dark}\) and use any common approach to get \(o_i\) and \(var_i\) for each pixel. As discussed below, we use an order-statistics approach to avoid any contamination from salt noise (e.g., cosmic rays hitting the pixels), but the most common would be to use the sample mean and variance to estimate the values of \(o_i\) and \(var_i\).
As Huang et al. note, the estimation for \(g\) can be cast as a least-squares minimization problem if we know \(o_i\), \(var_i\), and have a series of \(y\) obtained at several different exposure times and/or illumination intensities. However, their approach requires the use a pseudo-matrix inverse and is kind of annoying to program etc. Instead, here we show the equivalent maximum likelihood estimator of this problem, which is much easier to implement.
Note that both approaches assume for each \(k^{th}\) movie acquired, that
\[ \mathcal{N}(v^k_i-var_i \mid g(\bar{D^k_i}-o_i), \sigma^2_{least squares} ), \]
where the least squares variance is unimportant, but the same for each dataset. The MLE approach to this problem of estimating g is to take the derivative with respect to g of the log-likelihood (i.e., the product of these normal distributions), set that equal to zero, and solve for g. This gives
\[ \frac{d}{d g_i} \ln\mathcal{L} = 0 = \sum_k \left((v_i^k-var_i) - g(\bar{D_i^k}-o_i)\right) \cdot \left( -(\bar{D_i^k}-o_i)\right) \] \[ \sum_k \left(v_i^k-var_i \right)\left( g(\bar{D_i^k}-o_i) \right) = g_i \sum_k \left( g(\bar{D_i^k}-o_i) \right)^2 \]
\[ g_{i,MLE} = \frac{ \sum_k \left(v_i^k-var_i \right)\left( g(\bar{D_i^k}-o_i) \right)} { \sum_k \left( g(\bar{D_i^k}-o_i) \right)^2} \]
Checking this with our variables, we see that \[ g = \frac{\sum_k (g^2\lambda^{\prime\prime}t) (g\lambda^{\prime\prime}t)}{\sum_k (g\lambda^{\prime\prime}t)^2} \sim \frac{g^3}{g^2} \sim g^1.\]